二进制反射格雷码和Tromino问题Python代码实现

实现n位二进制反射格雷码（采用递归的减治法）

算法设计思想

  • n+1 位格雷码的前 2^n 个二进制串，可以由依此算法生成的 n 位格雷码(总共 2^n 个 n 位二进制串)按顺序排列，再在每个串前加一个前缀 0 构成。

  • n+1 位格雷码的后 2^n 个二进制串，可以由依此算法生成的 n 位格雷码(总共 2^n 个 n 位二进制串)按逆序排列，再在每个串前加一个前缀 1 构成。

具体步骤描述

  • 输入二进制反射格雷码的位数n

  • 递归调用BRGC_Recursion函数

  • n 等于1 时返回包含 0 和 1 字串的列表

  • n 不等于 1 时处理递归返回的列表

    • 先复制一份并翻转

    • 在原本返回的列表中的每个字串前添加 0

    • 在复制翻转后的列表中的每个字串前添加 1

    • 返回两个列表合并后的列表

实现源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
"""
二进制反射格雷码 -- 递归实现
输入：二进制反射格雷码位数n
输出：对应位数的二进制反射格雷码
"""
print("黄文焕 3190608027")
n = int(input("输入要生成的反射格雷码的位数："))


# 二进制反射格雷码递归函数定义
def BRGC_Recursion(n):
    if n == 1:
        return ['0', '1']
    else:
        res = BRGC_Recursion(n - 1)

        # 复制res
        res_cpy = res.copy()
        # 翻转res_cpy
        res_cpy.reverse()
        # 在res中每一项字串前拼接 '0'
        for i, v in enumerate(res):
            res[i] = '0' + v
        # 在res_copy中每一项字串前拼接 '1'
        for i, v in enumerate(res_cpy):
            res_cpy[i] = '1' + v
        # 返回res和res_copy拼接后的列表
        return res + res_cpy


# 输出生成的二进制反射格雷码
print(BRGC_Recursion(n))

运行结果截图

运行结果

实现n位二进制反射格雷码（非递归算法实现）

算法设计思想

  • 以全 0 的 n 位串开始。

  • 对于 i = 1,2,3 ,···, 2^(n-1), 则通过翻转前一位串中的第 b 位来生成第 i 个位串，前这里 b 是 i 的二进制表示中最低位 1 的位置

具体步骤描述

  • 输入二进制反射格雷码的位数n

  • 初始化结果列表中的第一个字串，为 n 个 0

  • 设置结束为 2 的 n 次方，遍历时则为 1 到 2^(n-1)

  • 将 i 转换成 n 位二进制字串

  • 从右向左寻找 i 的二进制字串中第一个 1 的索引

  • 将结果列表中最后一个字串中，对应索引位置的修改

    • 如果为 '1' 则换为 '0'，否则换为 '1'

实现源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
"""
二进制反射格雷码 -- 非递归实现
输入：二进制反射格雷码位数n
输出：对应位数的二进制反射格雷码
"""
print("黄文焕 3190608027")
n = int(input("输入要生成的反射格雷码的位数："))

# 初始化结果列表中的第一个字串，为n个0
res = ['0'*n]
# 设置结束为2的n次方
end = pow(2, n)
# 从1到end-1
for i in range(1, end):
    # 将i转换成二进制字串,去掉 '0b' 前缀
    i_bin = bin(i).replace('0b', '')
    # 并在i_bin前拼接 n-len(i_bin)长度个 '0'
    i_bin = '0' * (n - len(i_bin)) + i_bin
    # 将结果列表中最后一个字串转换成列表str
    str = list(res[i-1])
    # 在i_bin中从右向左寻找字符 '1'并返回对应索引
    index = i_bin.rfind('1')
    # 将str中对应索引的字符修改，如果为 '1' 则换为 '0'，否则换为 '1'
    str[index] = '0' if str[index] == '1' else '1'
    # 将str重新拼接成字符串，并添加入res列表
    res.append(''.join(str))

# 输出生成的二进制反射格雷码
print(res)

运行结果截图

运行结果

分治法实现2^n*2^n棋盘覆盖问题，棋盘用二维数组表示，缺失方块0填充，L型骨牌用相同整数填充。

算法设计思想

  • 将棋盘依次划分为四个象限，k所在象限继续划分。

  • k不在的剩余三个象限，将划分轴原点附近的剩余三个点，标志为L型骨牌

  • k不在的象限继续划分，并将之前标志为L型骨牌的点看做缺失点k

  • 依次类推，当划分棋盘大小size等于1时结束

具体步骤描述

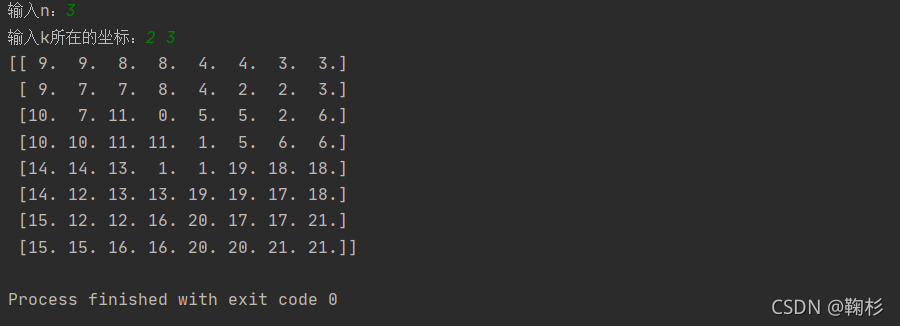
  • 输入 n 和 k 在棋盘中的坐标

  • 初始化棋盘

  • 将棋盘分为四个象限，k 所在的象限直接递归调用 Tromino

  • 对于 k 不在的三个象限，将划分轴原点附近的剩余三个点，标志为L型骨牌(以相同的数字表示)

  • k不在的象限继续划分，并将之前标志为 L型骨牌的点 看做缺失点 k

  • 依次类推，当划分棋盘大小size等于1时结束

实现源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
# 导入 numpy 包
import numpy as np

# 输入n和k在棋盘中的坐标
print("黄文焕 3190608027")
n = int(input("输入n："))
k_x, k_y = map(int, input("输入k所在的坐标：").split())

# 初始化棋盘
size = pow(2, n)
arr = np.ones((size, size))
arr_x, arr_y = arr.shape
arr[k_x][k_y] = 0

# 用于标注L形骨牌
num = 1

'''
参数说明：
    k_x, k_y -- k所在坐标
    arr_x, arr_y -- 起点坐标
    size -- 棋盘大小
算法思路：
    将棋盘依次划分为四个象限，k所在象限继续划分。
    k不在的剩余三个象限，将划分轴原点附近的剩余三个点，标志为L型骨牌
    k不在的象限继续划分，并将之前标志为L型骨牌的点看做缺失点k
    依次类推，当划分棋盘大小size等于1时结束
输入案例：
    输入n：3
    输入k所在的坐标：1 1
输出案例：
    [[ 9.  9.  8.  8.  4.  4.  3.  3.]
     [ 9.  0.  7.  8.  4.  2.  2.  3.]
     [10.  7.  7. 11.  5.  5.  2.  6.]
     [10. 10. 11. 11.  1.  5.  6.  6.]
     [14. 14. 13.  1.  1. 19. 18. 18.]
     [14. 12. 13. 13. 19. 19. 17. 18.]
     [15. 12. 12. 16. 20. 17. 17. 21.]
     [15. 15. 16. 16. 20. 20. 21. 21.]]

'''
# 定义Tromino递归函数
def Tromino(k_x, k_y, arr_x, arr_y, size):
    if size == 1:
        return
    D_size = int(size / 2)
    # 使用全局定义的num
    global num
    temp = num
    num += 1

    # 第一象限
    if k_x < arr_x + D_size and k_y >=arr_y + D_size:
        Tromino(k_x, k_y, arr_x, arr_y + D_size, D_size)
    else:
        arr[arr_x + D_size - 1][arr_y + D_size] = temp
        Tromino(arr_x + D_size - 1, arr_y + D_size, arr_x, arr_y + D_size, D_size)

    # 第二象限
    if k_x < arr_x + D_size and k_y < arr_y + D_size:
        Tromino(k_x, k_y, arr_x, arr_y, D_size)
    else:
        arr[arr_x + D_size - 1][arr_y + D_size - 1] = temp
        Tromino(arr_x + D_size - 1, arr_y + D_size - 1, arr_x, arr_y, D_size)

    # 第三象限
    if k_x >= arr_x + D_size and k_y < arr_y + D_size:
        Tromino(k_x, k_y, arr_x + D_size, arr_y, D_size)
    else:
        arr[arr_x + D_size][arr_y + D_size - 1] = temp
        Tromino(arr_x + D_size, arr_y + D_size - 1, arr_x + D_size, arr_y, D_size)

    # 第四象限
    if k_x >=arr_x + D_size and k_y >=arr_y + D_size:
        Tromino(k_x, k_y, arr_x + D_size, arr_y + D_size, D_size)
    else:
        arr[arr_x + D_size][arr_y + D_size] = temp
        Tromino(arr_x + D_size, arr_y + D_size, arr_x + D_size, arr_y + D_size, D_size)


# 调用Tromino函数
Tromino(k_x, k_y, 0, 0, size)

# 输出标注完成的棋盘
print(arr)

运行结果截图

运行结果
Algorithm
#Python #Binary Gray Code #Tromino
二进制反射格雷码和Tromino问题Python代码实现
https://hwh-2019.github.io/2022/12/03/二进制反射格雷码和Tromino问题Python代码实现/
作者
HWH
发布于
2022年12月3日
许可协议