加强Floyd算法和找零问题贪婪算法求解Python代码实现
加强Floyd算法,使得该算法能够求出最短路径本身,而不仅仅是它们的长度。
算法设计思想
所有路径都由两条路径构成: 一条从\(v_i\)到\(v_k\)的路径,路径中每个中间顶点的编号都不大于\(k-1\); 一条从\(v_k\)到\(v_j\)的路径,路径中每个中间顶点的编号也都不大于\(k-1\)
设路径长度为 \(d\) 得到以下递推式,\(当k\geq 1, d_{ij}^{(0)}=w_{ij}时, d_{ij}^{(k)} = min\begin{Bmatrix} d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)} \end{Bmatrix}\)
同理路径本身也可以得到与上面相同的公式
\[ E=mc^2 \]
具体步骤描述
初始化邻接矩阵
通过邻接矩阵来初始化路径矩阵
\(k\) 从 0 开始循环
遍历邻接矩阵,按照公式处理邻接矩阵和路径矩阵
\(当k\geq 1, d_{ij}^{(0)}=w_{ij}时, d_{ij}^{(k)} = min\begin{Bmatrix} d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)} \end{Bmatrix}\)
将两个矩阵返回,即得到最短路径的长度以及最短路径本身
实现源码
1 | |
运行结果截图

为找零问题写一个贪婪算法的伪代码,它以金额n和硬币的面额d1>d2>...>dm作为输入。
算法设计思想
- 将 n 和 d1 相除,商为硬币个数,再 n 取余 d1 赋值给 n,循环下去,直到 dm
具体步骤描述
输入 n 以及从大到小排列的币值
循环处理 li 中的币值,n / li[index],n = n % li[index]
将结果保存在字典 d 中,
返回结果字典 d
实现源码
1 | |
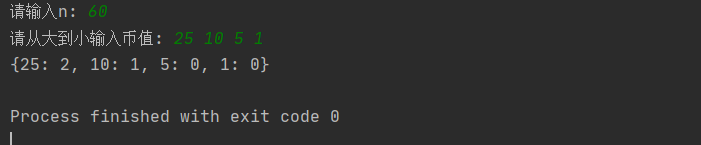
运行结果截图
加强Floyd算法和找零问题贪婪算法求解Python代码实现
https://hwh-2019.github.io/2022/12/03/加强Floyd算法和找零问题贪婪算法求解Python代码实现/